주뇽's 저장소
4. 확률변수와 확률분포 본문
4.1 확률변수와 확률분포의 정의
- 확률변수 (random variable) : 표본공간의 각 원소에 대응되는 실수 값
- 동전을 두 번 던지는 실험에서 표본공간 S = {HH, HT, TH, TT}
- 뒷면이 몇 번 나오는가에 관심이 있는 경우
- 동전의 뒷면이 나올 수 있는 횟수 = 0번, 1번, 2번
- 뒷면이 나오는 횟수와 숫자가 대응되는데, 이러한 숫자를 확률변수라고 하고 X라고 표기
간단하게 정리하자면 확률변수는 = 관심이 있는 사건이 생길 횟수이고 이 횟수는 시도횟수를 넘어갈 수 없다
ex) 동전을 세 번 던지다고 가정한다면 앞면이 나올 확률변수
0번 , 1번, 2번, 3번
이산, 연속표본공간
- 이산표본공간 (discreate sample space)
- 표본공간 S가 셀 수 있는 원소로 구성되어 있을 때
- 동전을 던지는 실험에 앞면이 나오는 회수, 100개의 제품 중 불량품의 수
- 이산확률분포 (discreate probability distribution)
- 이산표본공간에서 정의된 확률변수 X에 대한 함수
- 확률변수 X가 가질 수 있는 값 중에서 X = x에 대한 확률은 P(X = x) = f(x)로 나타냄
- 모든 x에 대하여 확률은 언제나 0이상의 값을 가지므로 f(x) ≥ 0
- 확률의 합은 1이므로 ∑ₓ f(x) = 1
#확률변수 (X) : 관심있는 사건이 생길 횟수
확률분포 (f(x)) : 관심있는 사건이 생길 횟수를 인자로 그 사건이 몇번 나오는지를
ex) 위의 동전을 세 번 던지는 실험을 예로 들면 X = 0,1,2,3이고 f(2) = 앞면이 2번 나올 확률
- 연속표본공간(continuous sample space)
- 표본공간을 연속된 실직선 상의 임의의 점으로 나타낼 수 있을 때
- ex) 키, 몸무게 , 제품의 수명
- 연속확률분포 (continuous probability distribution)
- 연속표본공간에서 정의된 확률변수 X에 대한 함수
- 모든 x에 대하여 확률은 언제나 0이상의 값을 가지므로 f(x) ≥ 0
- 확률의 합은 1이므로 ∫ f(x)dx = 1 (-∞ < x < ∞ )
- ex P(a < X < b) = ∫ f(x)dx 구간은 a 에서 b까지
- 연속표본공간에서 정의된 확률변수 X에 대한 함수
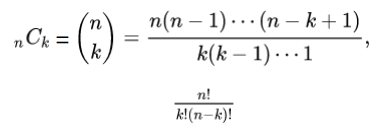
예제) 8개의 제품 중 3개의 불량품이 있을 때, 이 중 2개를 선택할 경우 불량품 개수 X에 대한 확률분포를 구하시오
확률변수 X : 총 2번을 골라서 불량품이 나오는 횟수 = {0번 ,1번, 2번}
먼저 0번 나올 확률분포(f(0)) 을 구해보면 위에 조합 공식을 사용해서 구한다면
불량품 3개 중 0개 * 양품 5개 중 2개 / 전체 8개중 2개를 뽑을 때 이렇게 정리할 수 있다. 다시 식을 정리하면
f(0) = ₃C₀ * ₅C₂ / ₈C₂ = 5 / 14
f(1) = ₃C₁ * ₅C₁ / ₈C₂ = 15 / 28
f(2) = ₃C₂ * ₅C₀ / ₈C₂ = 3 / 28
위 처럼 각각의 확률변수에 따라 확률분포를 구할 수 있다!
누적분포함수
- Cumulative distribution function
- 정의 : 확률변수 X가 어떤 x이하의 확률, F(x) = P(X ≤ x)
- 연속확률분포에서 확률값은 X가 값을 가지는 영역의 넓이로 정의한다.
- X가 정확히 특정 값 x일 확률 P(X = x) = 0 (선분의 넓이는 0)
- P (a < X ≤ b) = P(a < X < b) + P(X = b) = P(a < X < b)
- F(x) = P(X ≤ x) = P(X < x)
잘 이해가 되지 않는다 이해를 위해서 위에 예제의 누적분포함수를 한번 구해보면
확률변수 X = 0, 1, 2
각각의 누적확률
-F(0) = 5 / 14
-F(1) = f(0) + f(1) = 5 / 14 + 15 / 28 = 25 /28
-F(2) = f(0) + f(1) + f(2) = 5 / 14 + 15 / 28 + 3 / 28 = 1
결국 누적확률은 단어와 같이 그 확률변수 이하까지의 모든 확률의 합이라고 볼 수 있다!
그리고 모든 확률의 합은 1이다!!
확률분포함수
- 이산확률분포의 함수를 확률질량함수(PMF : probability mass function)
- 연속확률분포의 함수를 확률밀도함수(PDF : probability density function)
- 이를 합쳐서 확률분포함수(probability distribution function)
4.2 결합확률분포
- Joint probability distribution
- 2개 이상의 확률변수에 대한 확률분포를 의미
- 확률변수가 X와 Y인 경우 X와 Y의 주어진 영역 내에서의 확률분포는 f(x, y)로 나타낸다
- f(x, y) = P (X = x , Y = y) : 두 확률변수 X와 Y가 동시에 각각 x와 y의 값을 가질 확률
- 이산확률변수들의 결합확률분포는 확률변수 X와 Y가 이산적인 값을 갖게 되는 경우로 다음과 같은 조건을 만족
- 모든 x와 y에 대하여 확률은 언제나 0이상 1 이하의 값을 가지므로 0 ≤ f(x , y) ≤ 1
- 확률의 합은 1이므로 ∑ₓ ∑Y f(x, y) = 1
# 연속확률변수들의 결합확률분포 ∬f(x, y) = 1 ((-∞ < x , y < ∞ )
다음과 같은 예제로 확인을 해보자
예제) 주사위를 두 번 던지는 시행에서 3의 눈이 나온 횟수를 X라고 하고, 5의 눈이 나온 횟수를 Y라고 할 때 X와 Y의 결합확률분포 구하라 (이산확률)
#필요한 정보 정리
확률변수 X = {0, 1, 2}
확률변수 Y = {0, 1, 2}
#f(x, y)계산
-f(0,0) : 3도 안나오고 5도 안나올 확률 = 4/6 * 4 /6 = 16 / 36
-f(0,1) : 3은 한번도 안나오고 5는 한 번만 나올 확률 = (1/6 * 4/6 ) + (4/6 * 1/6) = 8 /36
-f(0,2) : 3은 한번도 안나오고 5는 두 번 모두 나올 확률 = (1/6 * 1/6) = 1/ 36
위와 같은 방법으로 나머지도 계산 가능
4.2.1 주변확률분포
- 확률변수 X와 Y로 구성된 결합확률분포 f(x, y)에서 각각의 주변확률분포 g(x) , h(y)는 다음과 같이 정의된다
- 이산확률변수인 경우 : g(x) = ∑(y) f(x, y), h(y) = ∑ₓ f(x, y)
- 연속확률변수인 경우 : g(x) = ∫ f(x, y)dy, h(y) = ∫ f(x,y)dx
(-∞ < x, y < ∞ ) # 관심있는 확률변수의 반대 값으로 계산!
#3장 주변확률과 같은 개념이지만 변수만 2개이상일 때 , 따라서 관심있는걸 제외하고 나머지 변수는 무시한다
다음과 같은 예제로 확인을 해보자
예제) 주사위를 두 번 던지는 시행에서 3의 눈이 나온 횟수를 X라고 하고, 5의 눈이 나온 횟수를 Y라고 할 때 X와 Y의 주변분포를 구하라 (이산확률)
# 제일 먼저 필요한 정보를 정리
주사위를 던질 수 있는 횟수(기회) = 2
확률변수 X = {0, 1, 2}
확률변수 Y = {0, 1, 2}
#g(x)부터 구해보자
g(0) : 주사위를 2번 던졌을 때 y는 관심이 없고 x(3)가 한번도 나오지 않을 확률
-g(0) = 5/6 * 5/6 = 25 / 36
g(1) : 주사위를 2번 던졌을 때 y는 관심이 없고 x(3)가 한 번만 나올 확률
-g(1) = (1/6 * 5 /6) + (5/6 * 1/6) → (첫 번째로 3이 나오고 다음은 안나올 확률) + (첫 번째로 안나오고 두 번째 3)
g(2) = 주사위를 2번 던졌을 때 y는 관심이 없고 x(3)가 두 번 모두 나올 확률
-g(2) = 1/6 * 1/6 = 1/36
같은 방식으로 h(y)도 구할 수 있다.
h(0) = 25 / 36
h(1) = 10 / 36
h(2) = 1 / 36
4.2.2 조건부확률분포
- 확률변수 X와 Y로 구성된 결합확률분포 f(x, y) 에서 조건부확률분포 f(x|y)는 다음과 같이 정의된다.
𝑓(𝑦 | 𝑥) = 𝑓(𝑥, 𝑦) / 𝑔(𝑥) , 𝑔 𝑥 > 0, 𝑓 (𝑥 | 𝑦) = 𝑓(𝑥, 𝑦) / ℎ(𝑦) , ℎ 𝑦 > 0
#𝑓(𝑦 | 𝑥) = x가 주어졌을 때 y에 대한 조건부확률분포
𝑓(𝑥, 𝑦) = 두 개의 확률변수의 결합확률
𝑔(𝑥) = x에 대한 주변확률
위의 주사위 예제로 이 조건부확률분포를 조금 더 이해해보자
예제) 주사위를 두 번 던지는 시행에서 3의 눈이 나온 횟수를 X라고 하고 , 5의 눈이 나온 횟수를 Y라고 할 때,
Y = 1로 주어졌다면 X의 조건부확률분포를 구하시오
#필요한 정보 정리
-𝑓(𝑥 | 𝑦) : y가 주어졌을 때 x에 대한 조건부확률 (현재 y = 1)
-𝑓(𝑥, 𝑦) : 주사위가 3 그리고 5가 동시에 나올 수 있는 확률 ( y는 무조건 한 번 나와야 한다)
-ℎ(𝑦) : x는 관심이 없고 y에 대한 주변확률분포
# 𝑓(𝑥 | 1)를 구해보자
-𝑓(𝑥 | 1) = 𝑓(𝑥, 1) / ℎ(1)
위에서 구했던 값을 가져오면 ℎ(1) = 10 / 36 따라서 10 / 36 * 𝑓(𝑥, 1)이다
- f(x,1) = y는 무조건 1번 나오고 x가 나올 확률을 구하면
x = {0, 1, 2} 이므로 하나씩 넣어서 구하자
f(0,1) = 3은 0번 5는 1번 나올 확률 = 8/36
f(1,1) = 3은 1번 5는 1번 나올 확률 = (1/6 * 1/6) + (1/6 * 1/6) = 2/36
f(2,1) = 3은 2번 5는 1번 나올 확률 = 0 (총 던질 수 있는 횟수는 2번이다)
따라서 f(0|1) = 36 / 10 * 8/36 = 8/10
f(1|1) = 36 / 10 * 2 /36 =2/10
f(2|1) = 36 / 10 * 0 = 0
조건부확률분포 = 결합확률분포 / 주변확률분포
4.2.3 확률변수의 독립
- 확률변수 X와 Y로 구성된 결합확률분포 f(x,y)에서 각각의 확률변수에 대한 주변확률분포 g(x), h(y)가
f(x,y) = g(x) * h(y)를 만족하면 확률변수 X, Y는 통계적으로 독립 이라고 하고, 역도 성립한다
# 3장에서와 마찬가지
결합확률 = 두 주변확률의 곱
결합확률분포 = 두 주변확률분포의 곱
4.3 확률변수의 기댓값으로서의 평균
- 확률변수의 기댓값(expected value, expectation)
- 각 사건이 벌어졌을 때의 확률변수의 값과 그 사건의 확률을 곱해 전체 사건에 대해 합한 값
- 어떤 확률적 사건에 대한 평균의 의미를 지님
- 이산확률변수 X의 평균 (기댓값)

- 연속확률변수 X의 평균 (기댓값)
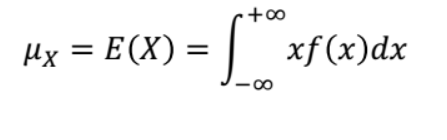
#예시#

위 예시를 한 번 보자
일단 공식에 대입을 하기 위해서 필요한 값들을 정리해보면 다음과 같다
X = +300 {HHH , TTT}
- 150 -(나머지)
각 원소가 발생 확률 = 1/8 f(x) = 1/8
f(x) = 2/8 (x=300)
6/8 (x=-150)
이제 공식에 대입해보면 [X(300) * f(x) (2/8) ] + [ X(-150) * f(x)(6/8) ]= -37.5 원이 된다
즉 이 게임은 평균적으로 37.5원씩 잃는 게임이다.
- 확률변수에 대한 함수의 평균

#예시 (이산확률변수)#

다음과 같은 특별한 확률을 가진 주사위가 있다고 가정하고
i(X) = 2X
f(x) = 각 주사위 확률
1~6까지 주사위가 나올 확률 * 배당금i(x) = 2x
공식에 대입 E(2X=i) = 25/3 이 나오는걸 확인 할 수 있다.
처음 배운 공식에 X자리에 i(X) 함수를 넣어주고 계산해주기만 하면 된다.
- 여러 확률변수에 대한 함수의 평균

#예시 (이산확률) #

3의 눈이 나올 확률 {0,1,2}
5의 눈이 나올 확률 {0,1,2}
한 쪽이 2가 나오면 나머지 한 쪽은 자동적으로 0이므로 나머지 항들만 계산하면
1 * f(1,1)만 계산해주면 된다.
- 여러 확률변수에 대한 함수의 평균 (주변화) #특수한 경우

# 두 개의 확률변수가 하나의 확률변수에만 종속되는 경우
- 확률변수의 기댓값의 성질

4.4 확률변수의 산포로서의 분산
- 분산은 그 확률변수가 기댓값으로부터 얼마나 떨어진 곳에 분포하는지를 가늠하는 척도
- 기댓값은 확률변수의 위치를 나타내고 분산은 그것이 얼마나 넓게 퍼져 있는지를 나타냄
- 분산보다는 분산의 제곱근인 표준편차가 더 자주 사용됨

확률변수 X의 확률분포가 f(x), 기댓값이 μ = E[X]일 때, X의 분산은,

# X-μ(X의 평균값) → X가 얼마나 떨어졌는지

# 간단히 정리 2장에서 표본분산을 정리한거와 마찬가지
##예시##

우선 평균값을 먼저 구하면 각각의 확률은 1/6로 동일하다 따라서 각 주사위가 나올확률은 7/2
이제 분산을 구하면 위 공식에 값을 대입
공식 : σ²=E(X²) - [E(X)]²
분산 = X²의 평균값 - X의 평균값의 제곱 → 35/12가 된다.
- 특정 확률변수에 대한 분산

##예시## 특정확률변수에 대한 분산

위 예제도 마찬가지로 첫 번째로 평균값을 구하고 그 평균값을 이용하여 분산값을 구하면 된다.
4.5 공분산
- 확률변수 X와 Y의 상관정도, 확률적으로 어떻게 결합되어 있는가를 나타내는 지표
- 두 확률변수의 결합확률분포가 f(x,y)일때, X와 Y의 공분산은
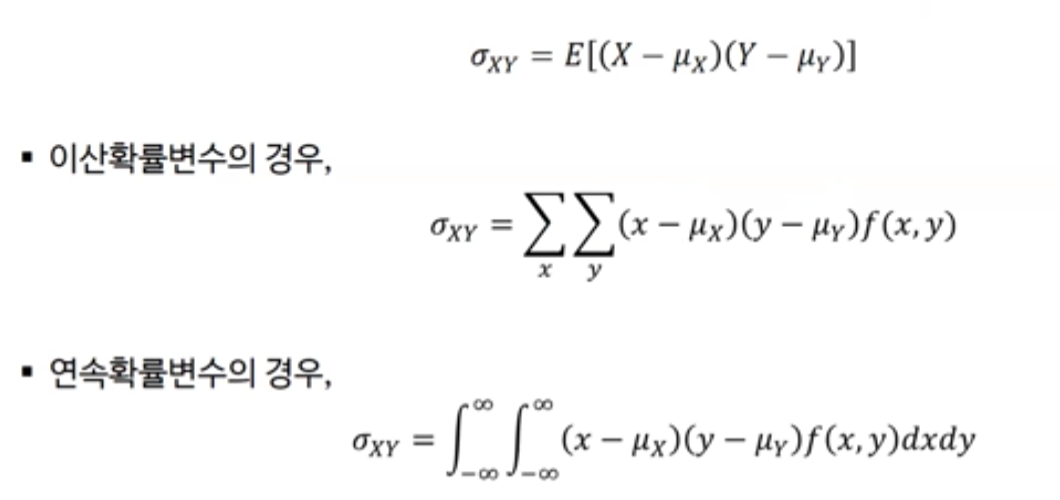

#공분산 공식 = E(XY) - E(X)E(Y)
공분산의 의미 : 공분산값이 양이면 X값이 커짐(작아짐)에 따라 Y값도 큰(작은) 값이 대응되는 관계를 나타내고, 공분산 값이 음이면 X값이 커짐(작아짐)에 따라 Y값은 작은(큰) 값이 대응되는 관계를 갖고 있다는 것을 의미한다.

###공분산 예시###

공분산 = E(XY) - E(X)E(Y) 을 이용하면
E(XY) = 2/36 , E(X) = 1/3 , E(Y) = 1/3 을 이용하면
2/36 - 1/9 = - 2/36 이 나오는 걸 확인 할 수 있다.
값이 -가 나왔으므로 3의 눈이 많이 나올 수록 5의 눈은 적게 나온다는 걸 확인 할 수 있다.
'응용통계학' 카테고리의 다른 글
| 5장 이산확률분포 (0) | 2021.11.09 |
|---|---|
| 3. 확률 (0) | 2021.10.23 |
| 2. 데이터의 정리와 요약 (0) | 2021.10.23 |




