주뇽's 저장소
3. 확률 본문
3-1 표본공간과 사건
- 표본공간(Sample space) : 실험(ex 동전, 주사위 던지기) 또는 관찰(ex 특정브랜드에 대한 선호 또는 거절)을 실시하여 나타날 수 있는 모든 결과의 집합 기호 S 를 사용
- 원소 : 표본공간을 구성하고 있는 요소들
- 사건(event) : 표본공간을 구성하고 있는 원소 중에서 관심의 대상이 되는 원소들이며 사건은 표본공간의 부분집합
- 여집합(complement) : S를 구성하고 있는 원소 중에서 사건 A에 포함되는 원소를 제외한 나머지 원소들의 집합
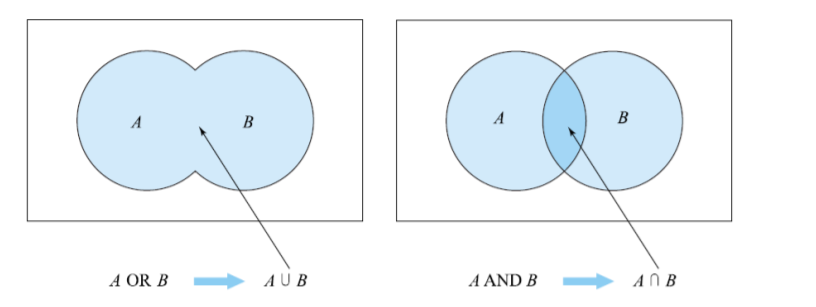
- 교집합(intersection) A∩B : A와 B가 동시에 발생할 수 있는 경우 (A and B)
- 합집합(union) A∪B : A 또는 B가 발생할 수 있는 경우 (A or B)
- 서로 배반(mutually exclusive) A∩B=∅ : 두 집합 A와 B의 공통되는 원소가 없는 경우
ex) 주사위를 던지는 실험에서 표본공간 S = {1,2,3,4,5,6}이고 이 표본공간은 S는 1부터 6까지 6개의 원소로 구성
이 때 짝수가 나오는 결과에만 관심이 있다면 사건 A = {2,4,6} , A의 여집합 = {1,3,5}이다. 이 때 3의 배수에만 관심이 있는 사건 B = {3, 6} 가 있다고 했을 때 A와B의 교집합은 A and B = {6} , A와B의 합집합은 A or B = {2,3,4,6}이 된다.
# 사건 A ={짝수} , 사건 B ={홀수}일 때 두 사건의 공통되는 원소가 없으므로 서로 배반이다 .
3-2 확률의 정의
- 고전적 확률의 개념(Classical definition of probability) : 프랑스의 수학자 피에르시몽 드 라플라스가 확률에 대한 개념의 필요성을 처음 주장
- 동전 던지기, 주사위 굴리기 등 표본공간이 유한할 때, 공간 내의 모든 사건이 동일하게 일어 날 수 있다 가정
- 어떤 사건의 발생 확률 = 그 사건이 일어날 수 있는 경우의 수 / 가능한 모든 경우의
- 논리적으로 옳아 보이지만 동전을 100번 던지면 각 면이 반드시 절반씩 나온다는 법이 없음
- John Venn, George Boole을 포함한 19세기의 수학자들은 의심을 풀었음
ex ) 동전에는 앞면과 뒷면의 각 면이 나올 가능성이 동일 하기 때문에 확률은 1/2이 되지만 100번을 던졌을 경우 50번은 앞면이 나온지 않는다.
상대도수 확률
- 빈도적 확률(frequentist probability) : 동전을 실제로 던져 보고 앞면이 나오는 횟수의 비율(상대도수)로 확률을 정해야 한다는 견해
- 동전을 던질 때마다 앞면이 나오는 횟수가 다르게 나오므로 한 개의 값으로 확률을 정할 수 없다는 문제점 존재
- 동전 던지는 일을 굉장히 많이 하면 상대도수 확률이 고전적 확률과 점차 가까워진다는 사실을 알게 됨
- 18세기 프랑스의 C.buffon은 4,040번의 동전을 던져 2,048번의 앞면을 얻어 그 상대도수 값이 0.5069가 됨을 얻음
- 1900년경 영국의 통계학자 K.Pearson은 24,000번의 동전을 던져 12,102번의 앞면을 얻어 0.5050의 상대도수을 얻음
- 2차 세계대전 중 독일군에 의해 포로가 된 남아프리카 통계학자 J.Kerrich는 수용소에서 생황을 하면서 10,000번의 동전을 던져 5,067번의 앞면 즉 0.5067의 상대도수 값을 얻음
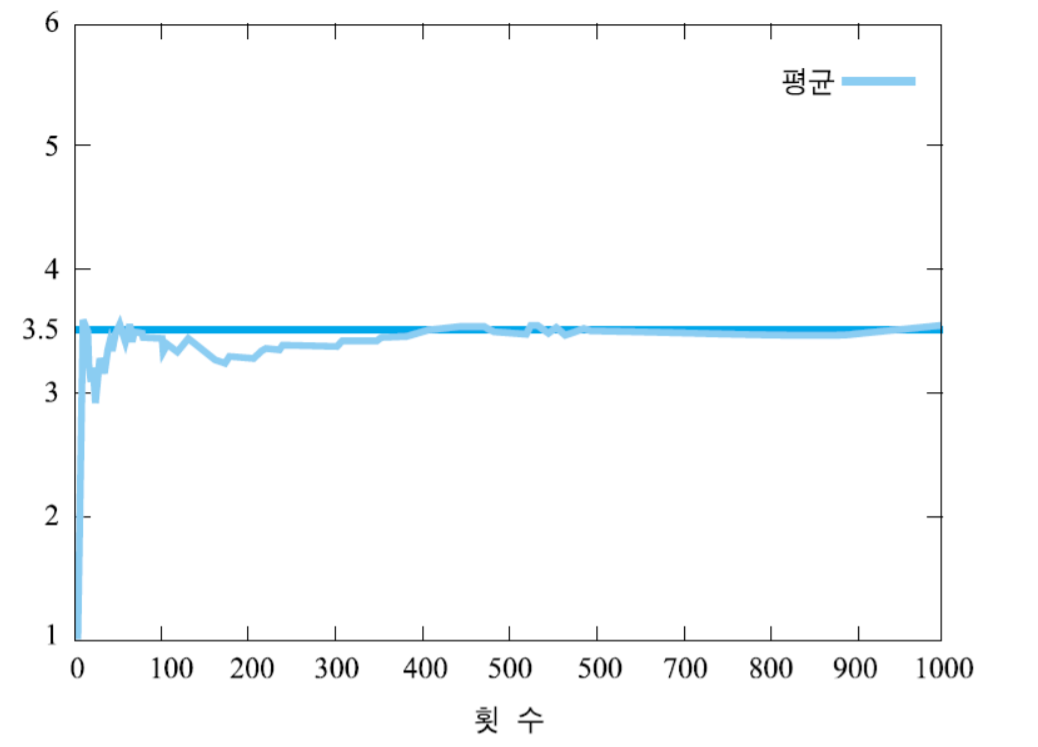
대수의 법칙
- Law of large number : 큰 수의 법칙
- 동일한 분포에서 무작위로 뽑은 표본이 많을수록 그 표본의 평균값은 이론적인 값에 가깝게 된다.
- 확률 = 상대도수의 극한 (n →∞)
- 스위스 수학자 베르누이에 의해 1713년에 증명
- 성공 또는 실패만이 있는 시행을 생각
- 성공의 확률을 p라고 함
- 아주 많은 수의 반복 시행을 하면 성공이 나올 가능성이 p에 수렴
확률의 정의
- 표본공간의 부분집한인 어떤 사건이 발생할 수 있는 가능성을 수치로 나타낸 것
- 표본공간의 모든 원소에 대한 확률의 합이 1이 되도록 배분
- 확률은 언제나 0이상 1이하의 값을 가짐
- 사건 A의 확률 P(A), P(S) =1 , 0 ≤ P(A) ≤ 1 , P(∅) = 0
합집합 사건의 확률 : A 사건 또는 B사건이 일어날 확률
- 표본공간 S의 부분집합 사건 A, B에 대해 𝐴 ∪ B의 확률은
–𝑃 (𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)
A 또는 B가 일어날 확률 = (A확률) + (B확률) - (A와B가 동시에 일어날 확률) - A,B가 서로 배반인 경우 𝑃 𝐴 ∩ 𝐵 = 𝑃 ∅ = 0, 𝑃(𝐴 ∪ 𝐵)= 𝑃 (𝐴) + 𝑃 (𝐵)
서로 동시에 일어날 확률이 없으므로 각각의 확률 값만 더해준다.
3-3 조건부 확률
결합확률
- 두 가지 사건이 동시에 일어날 확률 ( A and B)
ex) A사건 =3의 배수 , B사건 =짝수 주사위를 던졌을 때 두가지 사건이 동시에 일어날 확률
주변확률
- 여러 사건이 동시에 일어날 수 있을 때, 하나의 사건이 일어날 확률 분포
- 전체 확률 변수의 결합 분포를 기록한 표에서 각 행이나 열 단위로 원소들을 더한 값을 표의 주변에 써놓은 데에서 유래 하였다.
ex) 짝수가 뽑힐 확률 = 3/6 , 3의 배수가 뽑힐 확률 = 2/6 , 홀수가 뽑힐 확률 = 3/6
조건부 확률
- 어떤 사건 A와 B가 있을 때 이미 어떤 사건(조건)이 일어났고 나머지 사건이 일어날 확률
- 주어진 사건를 조건 혹은 사전 정보라고
ex) 주사위가 짝수 일 때(조건) 3의 배수가 나올 확률

# P(A|B) = B조건이 주어질 때 A사건이 일어날 확률 (조건부 확률)
P(B) = B가 일어날 확률
P(A ∩ B) = A사건과 B가 동시에 일어날 확률 (결합확률)
위 공식처럼 조건부 확률 = 특정사건A와 조건B가 동시에 일어날 확률을 B(조건)가 일어날 확률로 나눈 값이다
그렇다면 이제 배운것들을 종합해서 주사위가 짝수일 때 3의 배수가 나올 확률을 구해보면
일단 필요한 정보들을 정리해보면 다음과 같다.
# 조건부 확률 = P(B|A) : 주사위가 짝수일 때 3의 배수가 나올 확률
- S = 주사위 → {1, 2, 3, 4 ,5 , 6}
- A = 주사위가 짝수 → {2, 4, 6}
- B = 주사위가 3의 배수 →{3, 6}
- A ∩ B = 짝수이면서 3의 배수 →{6}
- P(A) = 짝수가 나올 확률 → 1/2 (6개 중 3개)
- P(B) = 3의 배수가 나올 확률 → 1/3 (6개 중 2개)
- P(A ∩ B) = 주사위가 짝수이고 3의 배수일 확률 → 1/6 (6개 중 1개)
이제 이 정보들을 공식에 그대로 대입시켜주자
P(B|A) = 결합확률 / 조건확률
(1/6) / (1/2) = 1/3 이 된다.
# P(B|A)일 때 B가 아닌 A가 조건이다 !! A가 주어질 때 B가 일어날 확률!! 혼동하지 않도록 조심하자
또한 이 공식을 이용하여 양 변의 조건확률을 곱해주면 결합확률을 구할 수 있다. 이 것을 승법공식이라 한다.
P(A and B) = P(B|A) x P(A)
사건의 독립
- 어떤 사건 A,B에 대해 두 사건이 독립(independent)이면
–𝑃 (𝐵|𝐴) = 𝑃(𝐵), 𝑃 (𝐴|𝐵) = 𝑃(𝐴) - 조건으로 주어진 사건 A/B가 다른 사건 B/A에 아무런 영향을 주지 못함(독립)
- 두 사건이 서로 독립이면 조건부 확률의 정의에 따라

따라서 승법공식을 이용하여 결합확률을 구하면
–𝑃 (𝐴 ∩ 𝐵) = 𝑃(𝐴) x 𝑃(𝐵) 결합확률 = 두 사건의 곱과 같다
# 사건이 독립일 때 두 사건의 결합확률은 두 사건의 곱과 동일하다.
'응용통계학' 카테고리의 다른 글
| 4. 확률변수와 확률분포 (0) | 2021.10.24 |
|---|---|
| 2. 데이터의 정리와 요약 (0) | 2021.10.23 |
| 제 1장 공학과 통계학 (0) | 2021.10.17 |



