주뇽's 저장소
2. 데이터의 정리와 요약 본문
728x90
반응형
2장은 데이터의 정리와 요약을 위한 여러가지 방법에 대해서 정리
- 도수분포표
- 히스토그램
- 중심위치의 척도
- 산토의 척도
- 각종 그래프
2-1 도수분포표(빈도)
- 변수값, 도수, 상대도수등을 알기 쉽게 표로 정리한 것
- 구성요소 : 제목, 측정단위, 측정값의 구간, 각 구간의 도수, 도수의 합계 등 측정값의
최소/최대값 / 범위 / 각 구간별 빈도, 분포의 모양등을 알 수 없다
- 나타내는 내용
- 계급 : 데이터의 전체 범위를 몇 개의 모집단위로 나눈 것, 목(적에 따라 숫자가 정해짐)
- 도수 : 각 계급에 속하는 데이터의 수
- 상대도수 : 도수/전체 데이터의 수 도수를 전체 데이터의 수로 나눈 값(특정구간에 많이 나올수록 1에 가까움)
- 만드는 단계
- 구간을 결정하기 위해 최소치 ,최대치를 구한다 (min, max)
- 구간의 개수는 일반적으로 7~15개 정도를 사용한다
- 구간의 간격은 max - min를 구간의 개수로 나눈값보다 약간 큰값을 결정한다.
- 편의상 최초 구간은 min(반올림) - (구간의 간격/2)를 시작점으로 정한다
- 대표치는 구간의 중위수를 나타낸다.
- 각 구간에 속하는 데이터의 수를 세어 정리한다.
2-2 체크시트
- 계수치(불량개수, 결점수 등)의 데이터가 분류항목 중 어디에 집되어 있나를 알아보기 위하여 데이터의 발생 형태를 기록하는 도구
- 데이터를 정확하고 쉽게 모을 수 있도록 하고 효과적인 분석이 가능하도록 데이터를 정리한다.
- 종류
- 계수표
- 분할표
- 위치도
2-3 히스토그램
- 계량치 데이터의 분포로 파악
- 표본 데이터로부터 모집단 분포의 특성을 추측하기 위함 (형태 , 중심위치 ,산포)
- 형태
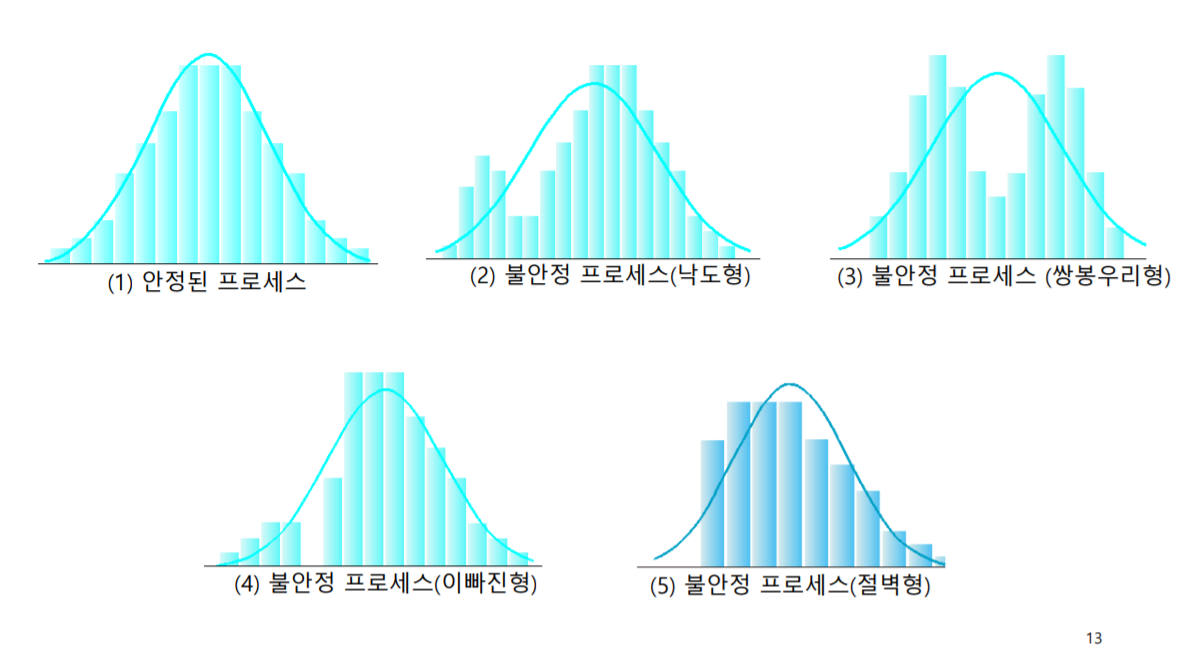
- 종모양 : 안정된 프로세스 ,도수가 중심 부근에 가장 많이 분포, 중심에서 멀어질수록 작아진다. 거의 좌우 대칭

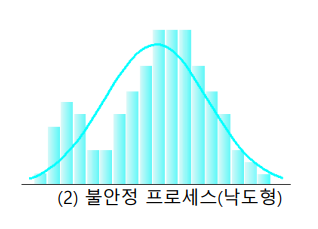
2.낙도형 : 히스토그램의 왼쪽 끝이나 오른쪽 끝에 외딴 데이터가 나타난다. 프로세스가 불안정하여 오염된 분포가
소량혼합된 형태
3. 쌍봉우리형 : 중심부근의 도수가 작아 산의 정상이 좌우로 나누어져 분포되어 있다. 프로세스가 두 가지 특성을 갖는 하부 프로세서들이 혼재한 경우에 발생하며, 이들을 분리(층화)하여 각각의 히스토그램을 작성한다.

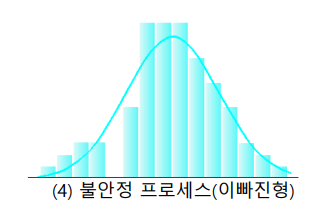
4. 이빠진형 : 계측기에 문제가 있어 특정 영역의 값이 측정되지 않는 경우에 발생한다.
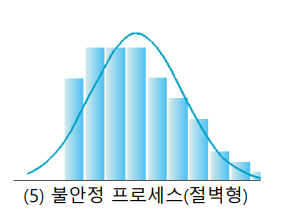
5.절벽형 : 평균값이 분포의 중심에서 극단적으로 한쪽에 치우쳐 있다. 측정/검사 시의 오류
ex) 어떤 경계치 이하 또는 이상의 제품을 제외한 경우)로 인해 발생한다.
2-4 중심위치의 척도
- 주어진 데이터가 있을때 데이터가 어떤 값을 중심으로 분포되어 있는가를 나타내는 양, 대표치
- 종류
- 평균(mean) : 각 데이터의 전체 합 / 데이터의 개수
- 중위수(median) : 데이터를 크기순으로 정렬하여 가운데 위치한 값(짝수이면 중앙값 두개의 합 /2)
- 최빈치(mode) : 가장 많이 발생한 숫자
- 기하평균(geometric mean)
- 조화평균 (harmonic mean)
- 절사평균 (trimmed mean) : 상 / 하위 10퍼씩 제외한 나머지 데이터의 평균 (올림픽 체조 점수 방식)
# 평균은 이상치(비정상적으로 크거나 작은 관측치)에 의하여 많은 영향을 받지만 중위수는 이상치에 무관하다.

위 그림처럼 A회사에 직원 1(이상치)때문에 A회사 직원들의 평균 월급이 높은것으로 나온다
이렇게 이상치가 있을때는 평균이 아닌 중위수를 사용하는 것이 모집단의 데이터를 판단하기에 좋다.
중심위치의 대표치를 선정하는 기준
- 명목척도 (성별, 전화번호) : 최빈치를 사용
- 순위척도 (순위 , 계급) : 중위수 사용
- 분포가 대칭적이고 이상점이 존재하지 않을 시 : 평균
- 비대칭이거나 이상치가 존재 : 중위수 (평균을 참고로 사용)
2-5 산포의 척도
- 데이터의 퍼짐(불균일성)정도를 나타낸다
- 표본 분산
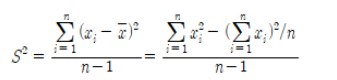
표본 분산 - 사분위수
- 데이터를 오름차순으로 정렬 후 4등분했을 경우의 값들
- 제1사분위수 (Q1): 오름차순 정렬된 데이터의 ¼에 해당, 1+0.25(n-1)번째 데이터의 값
- 제2사분위수 (Q2): 오름차순 정렬된 데이터의 ½ 에 해당, 중위수와 같은 값
- 제3사분위수 (Q3): 오름차순 정렬된 데이터의 ¾ 에 해당, 1+0.75(n-1)번째 데이터의 값
- 데이터가 정수번째가 아닌 경우, 선형 보간법 으로 계산
- 사분위수의 범위: Q3-Q1

2-6 각종 그래프
- 상자그림 : 분포의 중심위치와 치우침 정도 , 이상치의 유무를 판단
- 관측 데이터를 수평축에 점으로 나타냄
- 상자의 중앙에 중위수를 표시
- 상자의 위쪽이 제3사분위수(Q3), 아래쪽이 제1사분위수(Q1)
- 사분위수 범위 (Q3-Q1)의 1.5배 거리에 울타리(수염)를 나타낸 그림

- 산점도 : 두 변수(X,Y)의 상관관계를 연구하는데 사용
- 하나의 변수가 다른 변수의 원인이 됨을 증명하지는 못하지만 관계의 존재 여부
- 한 변수의 값이 변했을 때 다른 변수가 어떻게 변하는지 보여주기 위함. 두 변수의 관련성에 대한 가설을 세우고 검정하기 위한 예비 단계에서 사용될 수 있다.

- 파레토 그림 : 1897년 이탈리아 경제학자 Pareto가 20:80 법칙을 주장하면서 고안한 그림
치명적인 소수의 원인을 파악하고, 그 영향을 파악하도록 한 그림
ex) 80%의 기부금은 전체 기부자 20%가 기부한 금액- 데이터(예 : 불량건수 혹은 손실금액)의 분류 항목을 결정(원인 - 결과)
- 기간을 정하여 데이터를 수집
- 분류항목별로 데이터를 집계
- 가로축에 크기순으로 분류항목(원인)을 기입하고 세로축에 발생도수 혹은 상대도수(백분율)를 기입
- 세로축에 해당하는 막대그래프를 그린다.
- 누적상대도수(백분율)를 꺾은선 형태로 그림
- 수집기간, 기록자, 목적 등 관련 사항을 기입
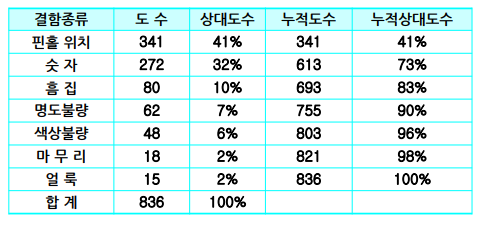
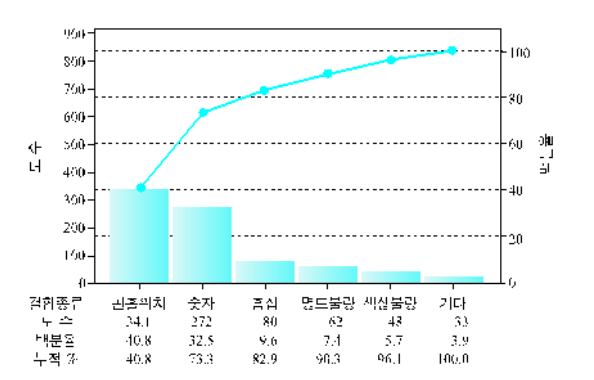
결함이 가장 많이 발생한 종류는 핀볼 위치와 숫자이다
이들만 제거한다면 결함의 약 73%를 방지할 수 있다.
- 관리도 : 런 그림의 한 종류
- 관리하고자 하는 대상(평균, 분산, 불량률, 결함율 등)에 대한 측정치를 관측 순서에 따라 타점하여 연결
- 관리 통계량의 기대치를 중심선으로 하고, 보통 표준편차의 3배씩 간격을 두어 한계선을 그림
- 관리 통계량이 한계선을 벗어나거나 이상한 패턴을 나타내면 프로세스에 이상이 발생한 것으로 판정

'응용통계학' 카테고리의 다른 글
| 4. 확률변수와 확률분포 (0) | 2021.10.24 |
|---|---|
| 3. 확률 (0) | 2021.10.23 |
| 제 1장 공학과 통계학 (0) | 2021.10.17 |



