주뇽's 저장소
동적계획법 (Dynamic programing) 본문
동적계획법
- 분할정복기법 (Divide - and - Conquer)과 유사하다.
- 문제를 여러 개의 subproblem으로 나누고, 각 subproblem을 해결한 후, 각 subproblem의 해답을 이용하여 원래 문제의 해답을 계산
- 각, subproblem이 독립적이지 않고, 서로 연관되어 있는 경우에는 매우 많은 반복연산이 이루어지고, 이로 하여금 많은 수행시간이 필요
ex) Fibonacci Numbers

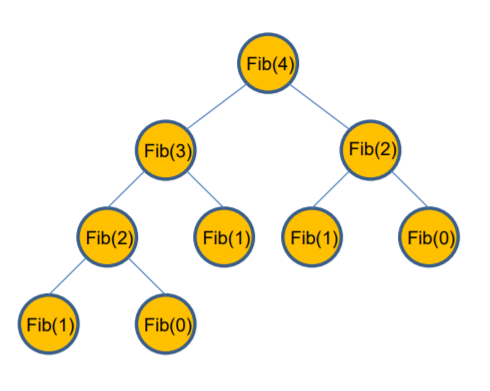
피보나치 수열은 초반에 재귀함수로 구현해본적이 있다. 분명 재귀적으로도 피보나치를 구할 수 있지만. 왜 동적프로그래밍에서 피보나치를 예시로 가져왔을까 ? 그 이유는 피보나치 수열은 계산도중 죽복되는 계산이 많이 발생한다는 점이 있다.! 초반에 언급한 subproblem이 독립적이지 않고, 서로 연관되어있다는 것이 바로 이 의미이다.
# fib(4)작아서 별로 감이 안 올 수 있지만 만약 fib(100)을 계산한다면 어떻게 될까 ?
밑에는 fib(n)을 계산할 때 덧셈의 횟수와 계산시간이다.

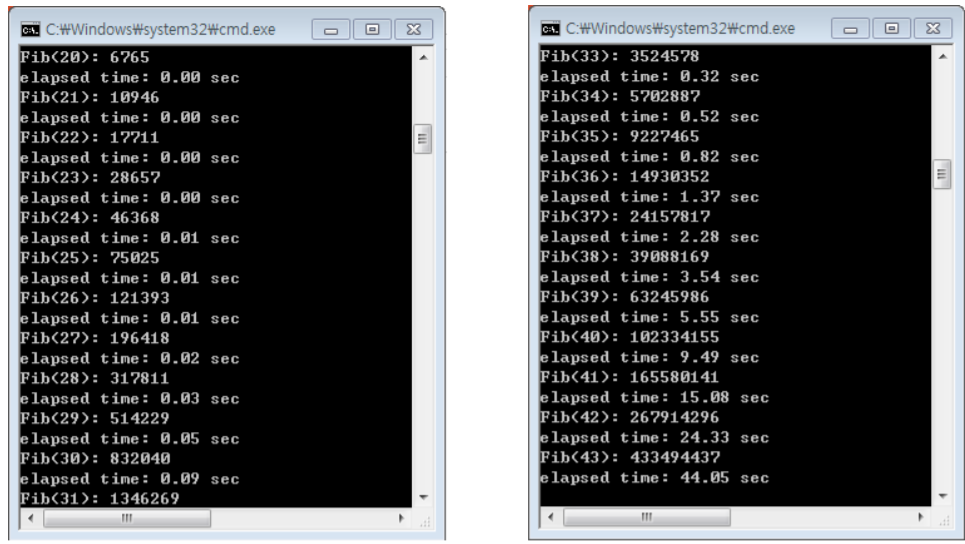
# fib(20) 까지만 해도 0.00초에 가까운 시간이 걸리지만 fib(40)은 44초나 걸린다.

#(왼)fib(35)계산시간은 약 1초가 걸린다 이 때 걸리는 시간이 fib수열과 똑같다 따라서 fib(72)의 계산시간은 fib(38)의 값과 같다라고 한다면 fib(72)의 계산시간은 39,088,169초 가 걸린다. *1년 = 31,536,000초
(오)fib(71)의 계산시간을 약 1년이라 한다면 다시 이 때 걸리는 시간이 fib수열과 똑같기 때문에 fib(100)의 계산시간은 fib(30)의 값과 같다라 한다면 결국 fib(100)의 계산시간은 832,040년이 걸린다!!
위와 같이 연산의 결과가 작을때는 몰랐지만 연산의 결과가 커지니 계산시간이 엄청나게 길어진다는걸 알 수 있다.
이 때 fib(n)같은경우 중복(반복)연산을 피해주기만 하는것으로 이 연산시간을 엄청나게 단축시킬 수 있다.
문제해결 방법
- Memoization(메모이제이션)
- 중복계산을 피하기 위해서 이미 계산된 값을 배열(캐시)에 저장해두는 것
- bottorm-up (바텀 업)방식
- 작은 데이터부터 시작하여 해답을 저장하여 큰 데이터의 해답을 찾는 것
'알고리즘 > 동적계획법(DP)' 카테고리의 다른 글
| 백준(BOJ) 다이나믹 프로그래밍 - 동전 1 (2293) - Gold5 (0) | 2023.08.25 |
|---|---|
| 백준(BOJ) 동적 계획법1 - 신나는 함수 실행(9184) Silver 2 (0) | 2023.08.14 |
| 백준(BOJ) 동적 계획법1 - 피보나치 1(24416) Bronze1 (0) | 2023.08.11 |



