주뇽's 저장소
8. 그래프 변형 CS224W: Machine Learning with Graphs 정리 본문
https://web.stanford.edu/class/cs224w
목차
1. 그래프 변형(Graph Manipulation)
- 특징(Feature) 수준의 그래프 변형 (Graph Feature Manipulation)
- 구조(Structure) 수준의 그래프 변형 (Graph Structure Manipulation)
👉 1. 그래프 변형(Graph Manipulation)

GNN에서는 일반적으로 입력 그래프를 그대로 사용하여 노드 임베딩을 학습한다. 하지만 항상 원본 그래프가 노드 임베딩을 학습하는 데 최적인 것은 아니다. 따라서 상황에 따라 그래프를 변형하여 사용하면 더 나은 성능을 얻을 수 있다.
그래프 변형이 필요한 이유는 크게 두 가지 관점에서 살펴볼 수 있다.
1. 특징(Feature) 관점:
- 문제 : 입력 그래프에 노드 특징 정보가 부족한 경우가 있다.
- 해결방법 : 특징 추가(Feature Agumentation)를 통해 노드 특징을 보완할 수 있다.
2. 구조(Structure) 관점:
- 그래프의 구조적 특성이 GNN 학습에 부적합한 경우가 있습니다. 예를 들면:
a) 그래프가 지나치게 희소(Sparse)한 경우:
- 문제 : 메시지 전달이 비효율적일 수 있습니다.
- 해결방법 : 가상의 노드나 엣지를 추가하여 그래프 밀도를 높일 수 있다.
b) 그래프가 지나치게 조밀(Dense)한 경우:
- 문제 : 메시지 전달의 계산 비용이 매우 높아질 수 있다.
- 해결방법 : 메시지 전달 시 이웃 노드를 샘플링하여 계산 비용을 낮출 수 있다.
c) 그래프가 매우 큰 경우:
- 문제 : 큰 그래프를 통째로 GNN에 입력하기 어려울 수 있다. (메모리 제약)
- 해결방법 : 임베딩 계산을 위해 그래프에서 하위 그래프(Subgraph)를 샘플링할 수 있다.
- 특징(Feature) 수준의 그래프 변형 (Graph Feature Manipulation)
- 입력 그래프에 노드 특징 정보가 없는 경우
- 이는 인접 행렬(Adjacency Matrix)만 있고 노드 특징 행렬(Node Feature Matrix)이 없는 경우에 해당한다
이러한 경우 노드 특징을 추가하는 일반적인 방법으로는 다음 두 가지가 있다:
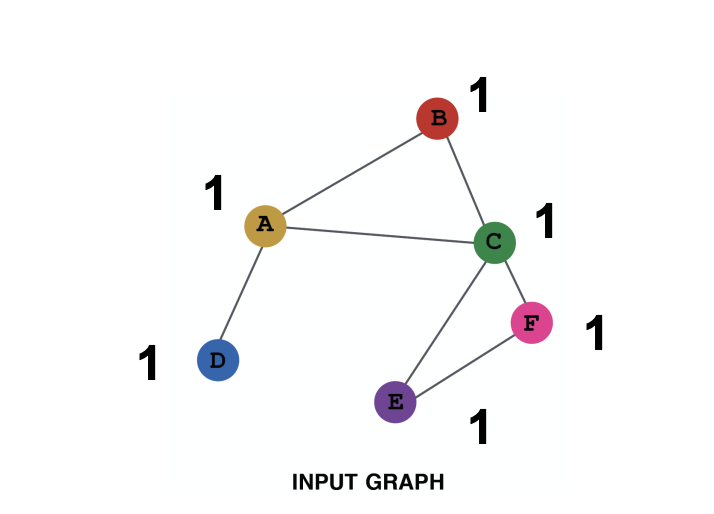
a) 모든 노드에 동일한 상수 값 할당하기:
- 예를 들어, 모든 노드에 1을 할당한다.
- 이 경우 노드 특징 행렬은 모든 원소가 1인 행렬이 된다.
b) 각 노드에 고유한 ID 할당하기:
- 그래프의 각 노드에 1부터 N까지의 고유한 ID를 부여한다. (N은 노드 수)
- 각 노드의 ID를 One-hot 벡터로 변환한다.
- 예를 들어, ID가 3인 노드는 [0, 0, 1, 0, ..., 0]과 같은 벡터로 표현 다.
- 이 경우 노드 특징 행렬은 N×N 크기의 단위 행렬(Identity Matrix)이 된다.

| 특징 종류 | 상수 노드 특징 | One-hot 노드 특징 |
| 표현력 | 중간. 모든 노드가 동일한 특징을 가지지만, GNN은 그래프 구조로부터 학습 가능 | 높음. 각 노드가 고유한 ID를 가지므로 노드 별 정보 저장 가능 |
| 귀납적 학습 (새로운 노드로의 일반화) |
높음. 새로운 노드에 상수 특징을 부여하고 GNN을 적용하는 것이 간단함 | 낮음. 새로운 노드는 새로운 ID를 가지므로, GNN이 이를 처리하는 방법을 학습하기 어려움 |
| 계산 비용 | 낮음. 특징 차원이 1이므로 효율적 | 높음. 특징 차원이 노드 수에 비례하므로 큰 그래프에는 적용 어려움 |
| 적용 상황 | 모든 그래프. 특히 귀납적 학습(새로운 노드로의 일반화)이 필요한 경우 | 작은 그래프. 귀납적 학습이 필요 없는 경우 |
- 일반적으로는 큰 그래프나 새로운 노드 추가가 빈번한 경우 상수 노드 특징을,
- 작은 그래프이며 노드 추가가 없는 경우 One-hot 노드 특징을 사용하는 것이 효과적이다.
- 구조(Structure) 수준의 그래프 변형 (Graph Structure Manipulation)
1. 그래프가 지나치게 희소(Sparse)한 경우:
- 그래프의 연결이 너무 적으면 메시지 전달이 원활하게 이루어지지 않을 수 있다.
- 이런 경우 가상의 노드나 엣지를 추가하여 그래프의 밀도를 높일 수 있다.
a) 가상 엣지 추가:
- 자주 사용되는 방법 중 하나는 2-hop 이웃을 가상 엣지로 연결하는 것이다.
- 즉, 원래 그래프의 인접 행렬 A 대신 A + A^2를 사용하는 것과 같다.
- 이는 두 노드 사이의 연결 관계를 보다 풍부하게 표현할 수 있게 해준다.
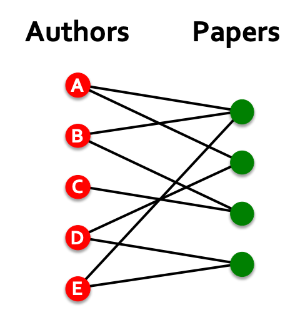
- 특히 저자-논문 관계와 같은 이분 그래프(Bipartite Graph)에서 유용하다.
- 가상 엣지를 통해 저자 간 연결 관계(공저자 관계)를 나타낼 수 있기 때문이다.
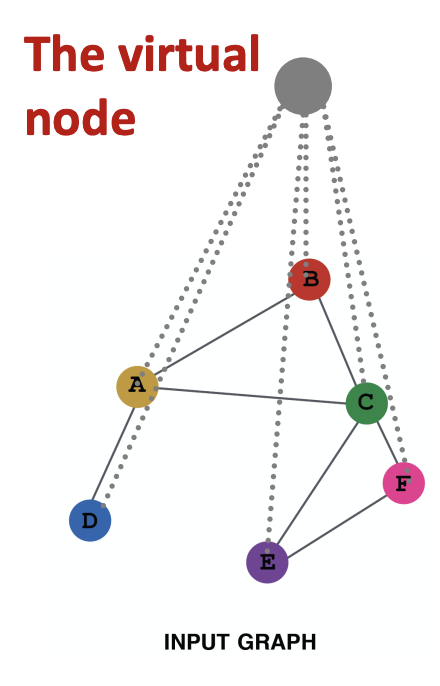
b) 가상 노드 추가:
- 그래프에 가상의 노드를 추가하는 것이다.
- 가상 노드는 그래프의 모든 노드와 연결된다.
- 예를 들어, 희소 그래프에서 두 노드 사이의 최단 경로 거리가 10이라고 하면 가상 노드를 추가하면 모든 노드 쌍 사이의 거리가 2로 줄어든다.
- (노드 A - 가상 노드 - 노드 B의 경로를 통해 연결되므로)
- 이는 희소 그래프에서의 메시지 전달을 크게 향상시켜 준다.
2. 그래프가 지나치게 조밀(Dense)한 경우:
- 그래프의 연결이 너무 많으면 계산 비용이 크게 증가할 수 있다.
- 특히 허브 노드(차수가 매우 높은 노드)가 존재하는 경우 문제가 된다.
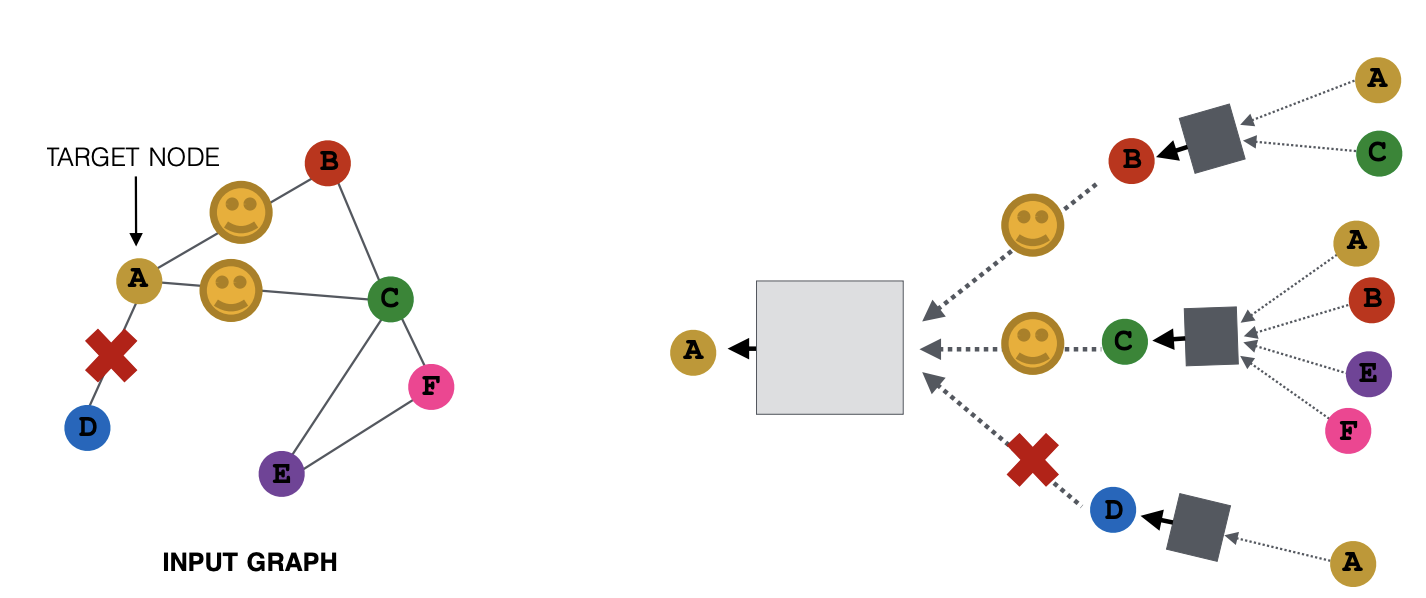
- 이런 경우 메시지 전달 시 이웃 노드를 샘플링하여 계산 비용을 줄일 수 있다.
- 예를 들어, 각 노드가 메시지 전달에 사용할 이웃 노드를 랜덤하게 2개만 선택할 수 있다.
- 매번 임베딩을 계산할 때마다 서로 다른 이웃 노드 집합을 랜덤하게 선택
- 이웃 샘플링을 통해 전체 이웃을 사용하는 것과 유사한 효과를 기대할 수 있다. 매 번 샘플링된 이웃 집합은 달라지지만, 여러 번 임베딩을 계산하면 결과적으로 모든 이웃의 정보가 고려될 수 있기 때문이다.


3. 그래프가 매우 큰 경우:
- 노드 수가 매우 많은 거대한 그래프의 경우, 전체 그래프를 한 번에 처리하기 어려울 수 있다.
- 이런 경우 그래프에서 하위 그래프(Subgraph)를 샘플링하여 임베딩을 계산할 수 있다.
- 하위 그래프는 전체 그래프의 특성을 잘 반영하도록 선택되어야 한다.
- 이를 통해 계산 자원의 한계를 극복하면서도 효과적인 노드 임베딩을 학습할 수 있다.
📝 정리
GNN에서는 주어진 그래프를 그대로 사용하기보다 상황에 맞게 그래프를 변형하여 사용하면 더 나은 성능을 얻을 수 있다. 그래프 변형은 크게 특징(Feature) 수준과 구조(Structure) 수준에서 이루어진다.
특징 수준의 그래프 변형:
- 입력 그래프에 노드 특징 정보가 부족한 경우 사용.
- 모든 노드에 동일한 상수 값을 할당하거나, 각 노드에 고유한 ID를 부여하는 방식으로 특징을 추가.
- 상수 값 할당은 계산 효율적이고 귀납적 학습에 유리하지만, 노드 구분이 어려움.
- 고유 ID 할당은 노드 구분에 유리하지만, 계산 비용이 높고 귀납적 학습에 불리함.
구조 수준의 그래프 변형:
1. 희소 그래프인 경우:
- 가상 엣지 추가: 2-hop 이웃을 연결하여 그래프 밀도를 높임. 특히 이분 그래프에서 유용.
- 가상 노드 추가: 모든 노드와 연결된 가상 노드를 추가하여 노드 간 거리를 줄이고 메시지 전달을 향상.
2. 조밀 그래프인 경우:
- 이웃 샘플링: 메시지 전달 시 이웃 노드를 랜덤하게 샘플링하여 계산 비용을 줄임.
- 샘플링을 통해 전체 이웃 사용과 유사한 효과를 얻을 수 있음.
3. 거대 그래프인 경우:
- 하위 그래프 샘플링: 전체 그래프에서 일부 하위 그래프를 샘플링하여 임베딩을 계산.
- 계산 자원 한계를 극복하면서도 효과적인 임베딩 학습이 가능.
그래프 변형은 GNN의 성능 향상에 중요한 역할을 한다. 특징 추가를 통해 노드 구분 능력을 높이고, 구조 변형을 통해 GNN 학습의 효율성과 효과성을 개선할 수 있다. 따라서 GNN을 적용할 때는 항상 그래프 변형의 필요성을 검토하고, 적절한 변형 기법을 활용하는 것이 좋다.
'GNN > CS224' 카테고리의 다른 글
| 9. GNN 학습(1) Prediction-head CS224W: Machine Learning with Graphs 정리 (2) | 2024.04.12 |
|---|---|
| 7. 다층 GNN 레이어 CS224W: Machine Learning with Graphs 정리 (0) | 2024.04.11 |
| 6. Graph Neural Networks(2) CS224W: Machine Learning with Graphs 정리 (0) | 2024.04.03 |





