주뇽's 저장소
7. 다층 GNN 레이어 CS224W: Machine Learning with Graphs 정리 본문
https://web.stanford.edu/class/cs224w
목차
1. 다층 GNN Layer (Layer connectivity)
2. Over-Smoothing 문제
- 수용필드(Receptive field)
3. 얕은 GNN 레이어의 문제를 해결하는 방법
- MLP
- Skip Connection
👉 1. 다층 GNN Layer (Layer connectivity)

단일 GNN 레이어를 다층 GNN 레이어로 만드는 가장 기본적인 방법은 GNN레이어를 순차적으로 쌓는것이다.
- Input : 초기 V노드의 특성 Xv
- Output : L번의 레이러를 통과한 임베딩 벡터 Hv^(L)

GNN에서의 레이어의 개념은 정보를 수집하기 위해 얼마나 많은 홉을 이동해야 하는지에 대한 정보이다. 이 때 너무 많은 이동을 하게 된다면 즉, 레이어가 깊어진다면 모든 노드들은 서로 연결이 되어버리면서 모든 노드들의 특성이 같은 값으로 수렴하게 된다. 이러한 문제를 Over-Smooting 문제라고 한다.
👉 2. Over-Smoothing 문제
우리는 서로 다른 노드 임베딩값을 가지기를 원하지만 GNN의 레이어가 깊어지면서 모든 노드의 임베딩 값이 같은 값으로 수렴하게 되는 Over-Smooing문제가 발생한다. 그렇다면 도대체 왜 이러한 문제가 발생할까? 이 질문에 대답하기 위해서는 우선 수용필드(Receptive field)라는 개념을 알아야 한다.
- 수용필드(Receptive field)
수용필드란 관심있는 노드의 임베딩을 결정하는 노드의 집합이라고 설명할 수 있다. 아래 이미지를 보면 이해하기 편하다.
- K-layer GNN은 각각의 K-hop의 이웃을 가진 수용필드를 가지게 된다.
- 노란 노드 : 우리가 관심있어 하는 노드
- 빨간 노드 : 수용필드라 하며 노란 노드와 K 홉으로 연결되어 있는 노드
- 회색 노드 : 그 외에 노드

3개의 레이어 모두 우리가 관심있어 하는 노란노드는 동일하므로 빨간 노드 중점으로 비교해보면 다음과 같다.
- 1-Layer GNN 수용필드
- 빨간 노드 : 노란 노드와 1홉 연결되어 있는 노드 (5개 노드)
- 2-Layer GNN 수용필드
- 빨간 노드 : 노란 노드와 2홉(1홉을 포함) 연결되어 있는 노드(30개 노드)
- 3-Layer GNN 수용필드
- 빨간 노드 : 노란 노드와 3홉(1홉, 2홉을 포함) 연결되어 있는 노드(거의 모든 노드)
위 예제와 같이 K=3일 때 수용필드를 보면 빨간 노드가 그래프와 비슷하게 된다.
즉, 수용필드가 커질수록 수용필드가 크게 겹치는 노드들은 유사한 임베딩을 가지게 된다
- 노란 노드 : 우리가 관심있어 하는 노드들
- 빨간 노드 : 2개의 노란노드와 공유된 이웃노드
- 회색 노드 : 그 외에 노드
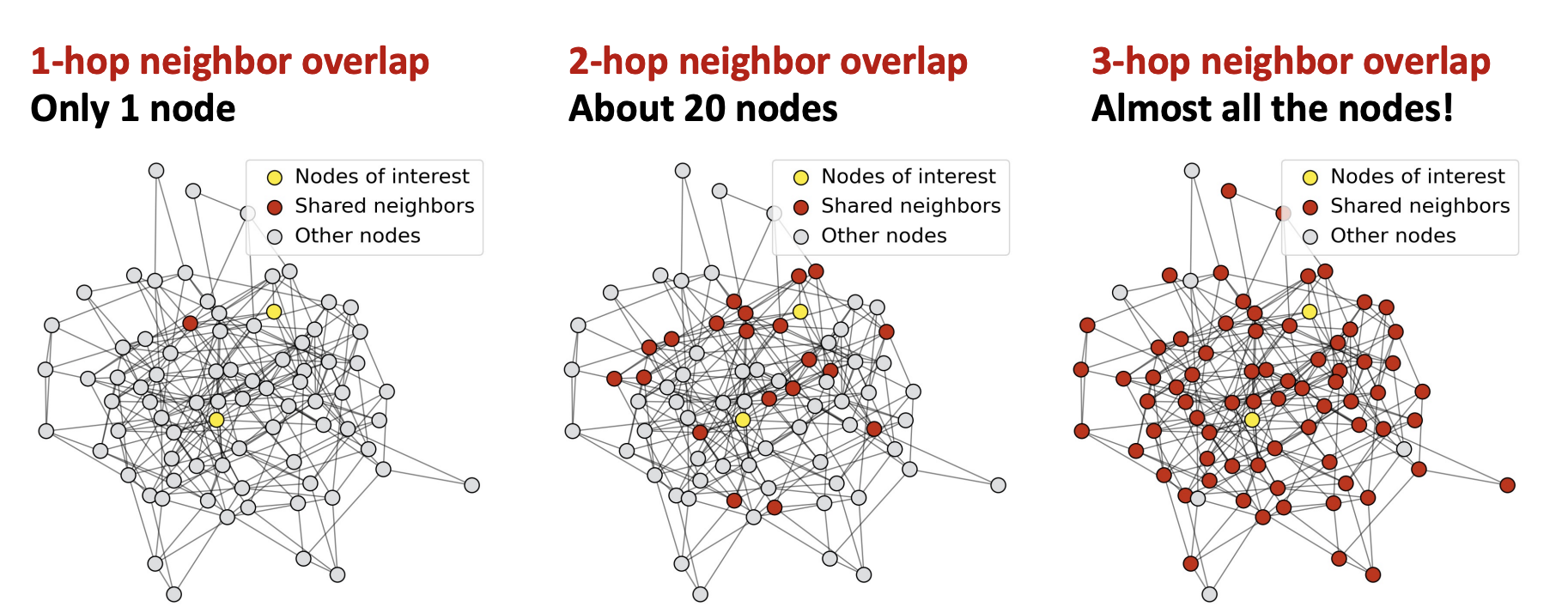
- 1-hop 겹친 이웃
- 빨간 노드 : 1홉의 경우 공유된 이웃노드는 1개
- 2-hop 겹친 이웃
- 빨간 노드 : 2홉의 경우 공유된 이웃노드는 약 20개
- 3-hop 겹친 이웃
- 빨간 노드 : 3홉의 경우 거의 모든 이웃을 공유하게 된다
위처럼 GNN의 레이어가 깊어질수록 공유하는 이웃들이 많아진다면 결국 개인의 고유한 특성보다는 네트워크 전체의 평균적인 특성이 모든 노드 임베딩을 지배하게된다. 이러한 over-smooting문제를 해결하기 위해서는 GNN레이어를 얕게 쌓을 수 밖에 없다. 하지만 얕은 레이어를 쌓는다면 그만큼 표현력이 부족해진다. 이러한 얕은 GNN 레이어의 문제를 해결하는 방법은 없을까?
👉 3. 얕은 GNN 레이어의 문제를 해결하는 방법
- MLP
GNN 레이어를 얕게 쌓으면서 생기는 표현력 부족의 문제를 GNN 레이어 내부에서 해결하는 방법이다.
이전 GNN 레이어의 경우에서는 각각의 메시지를 변환하거나 변환된 메시지를 집계하는 과정에서 오직 하나의 선형 레이어만을 사용했다. 이를 여러개의 Multi-Layer로 연결하는 것이다.
Solution 1 : 각각의 GNN 레이어안에 MLP를 추가
- 기존 메시지 변환 : W가중치 행렬과 노드 임베딩 hv를 행렬곱 연산
- 기존 메시지 집계 : 위 메시지 변환을 통해 나왔던 임베딩 값을 Sum, Mean등을 이용해 연산
위 선형연산으로만 이루어진 2개의 과정에 각각 선형 연산 + 비선형 연산(활성화 함수)를 이용하여 표현력을 증가하고 이를 통해 노드 간 상호작용을 더 풍부하게 모델링할 수 있다.
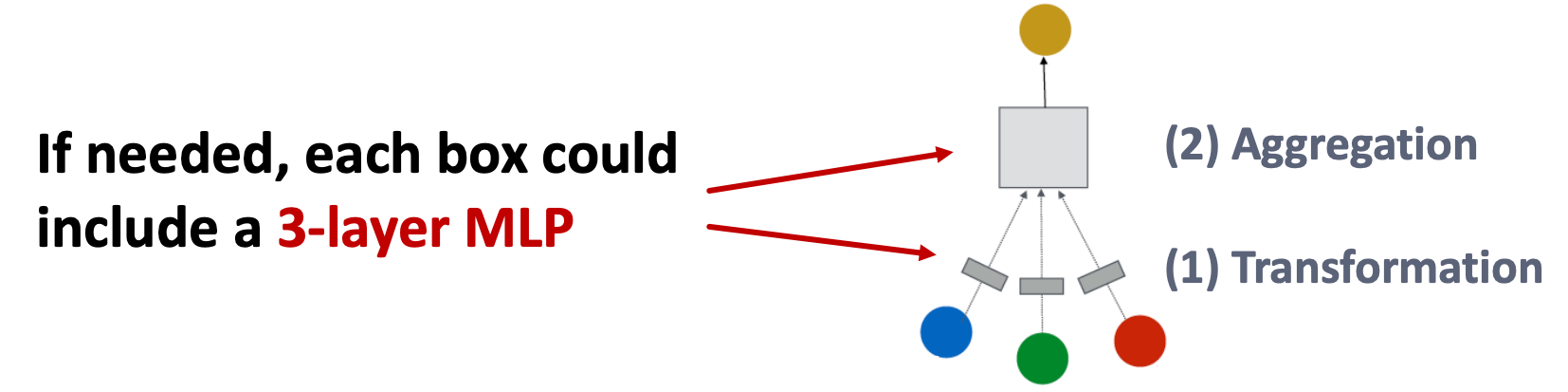
Solution 2 : GNN은 GNN layers만을 포함해야하는것은 아니다.

- Pre-processing layers : 그래프의 노드 특징(feature)을 초기에 변환하는 역할 (nodes represent images/text)
- Post-processing layers : 노드를 통한 예측/변환 임베딩이 중요한 경우(graph classification, knowledge grphas)
- Skip Connection
MLP를 쌓는 과정에서 Resnet에서 사용된 Skip Connetcion 아이디어를 가져와서 사용한다.
Solution 1 : 레이어 간 Skip Connection:


ResNet과 유사한 방식으로, GNN 레이어 사이에 직접적인 연결을 추가한다. 이런 방식의 Skip Connection은 GNN에서 다음과 같은 장점을 가져다 준다.
- 기울기 소실(Vanishing Gradient) 문제를 완화하여 더 깊은 GNN을 학습할 수 있게 해준다.
- 얕은 GNN과 깊은 GNN을 동시에 학습하는 것과 같은 효과를 얻을 수 있다.
Solution 2 : 초기 레이어에서 마지막 레이어로의 Skip Connection:

모든 중간 레이어를 건너뛰고 초기 레이어의 노드 임베딩을 직접 마지막 레이어에 전달하는 방식이다. 초기 레이어의 정보가 마지막 레이어까지 직접 전달될 수 있기 때문에 GNN의 수용 영역(Receptive Field)을 크게 넓혀준다.
Skip Connection 효과
- 기울기 흐름 개선:
- Skip Connection은 기울기가 레이어를 건너뛰어 직접 전달될 수 있는 경로를 제공하여 기울기 소실 문제를 완화하고, 더 깊은 GNN을 효과적으로 학습할 수 있게 한다.
- 다양한 수용 영역:
- Skip Connection은 다양한 길이의 경로를 만들어낸다. 이는 GNN이 여러 크기의 수용 영역을 동시에 고려할 수 있게 해준다.
- 앙상블 효과:
- Skip Connection으로 인해 GNN은 사실상 여러 개의 얕은 네트워크와 깊은 네트워크를 앙상블하는 것과 같은 효과를 얻게 된다. 이는 모델의 일반화 능력을 향상시킬 수 있다.
📝 정리
GNN에서 레이어를 쌓는 가장 기본적인 방법은 GNN 레이어를 순차적으로 쌓는 것이다. 하지만 레이어가 깊어질수록 Over-smoothing 문제가 발생하게 된다.
Over-smoothing 문제는 GNN의 레이어가 깊어질수록 모든 노드의 수용필드(Receptive field)가 서로 겹치면서 결국 모든 노드의 임베딩이 같은 값으로 수렴하게 되는 현상을 말한다.
이 문제를 해결하기 위해서는 GNN 레이어를 얕게 쌓을 수밖에 없는데, 이렇게 되면 모델의 표현력이 제한된다는 단점이 있다.
얕은 GNN 레이어의 표현력 문제를 해결하기 위한 방법으로는 크게 두 가지가 있다.
첫째, GNN 레이어 내부의 메시지 변환 및 집계 과정에서 단순 선형 변환 대신 MLP를 사용하는 것이다. 이를 통해 각 레이어의 표현력을 높일 수 있다.
또한 GNN은 순수한 GNN 레이어 외에도 입력 그래프의 노드 특징을 초기에 변환하는 Pre-processing layers와 출력 노드 임베딩을 Task에 맞게 변환하는 Post-processing layers를 포함할 수 있다.
둘째, Skip Connection을 활용하는 것이다. GNN 레이어 사이에 직접 연결을 추가하거나(레이어 간 Skip Connection), 초기 레이어에서 마지막 레이어로 바로 연결하는 방식(초기-마지막 레이어 Skip Connection)으로 Skip Connection을 구현할 수 있다.
Skip Connection은 기울기 소실 문제를 완화하고, 다양한 수용 영역을 고려할 수 있게 해주며, 앙상블 효과를 통해 모델의 일반화 능력을 향상시킨다.
결론적으로, GNN 설계 시에는 Over-smoothing 문제를 고려하여 적절한 레이어 수를 설정하고, 레이어 내부에 MLP를 도입하거나 필요에 따라 Pre/Post-processing layers를 활용하는 것도 도움이 될 수 있다. 또한 Skip Connection을 활용하여 모델의 표현력과 일반화 능력을 높이는 것이 중요하다.
'GNN > CS224' 카테고리의 다른 글
| 8. 그래프 변형 CS224W: Machine Learning with Graphs 정리 (0) | 2024.04.12 |
|---|---|
| 6. Graph Neural Networks(2) CS224W: Machine Learning with Graphs 정리 (0) | 2024.04.03 |
| 5. Graph Neural Networks(1) CS224W: Machine Learning with Graphs 정리 (4) | 2024.03.26 |




