주뇽's 저장소
[활성화 함수] 다중 분류 Task에서 자주 사용되는 소프트맥스(Softmax) 본문
분류
분류 문제란 주어진 입력 데이터를 미리 정의된 몇 개의 클래스 또는 범주 중 하나로 할당하는 문제를 말한다. 이는 기계 학습, 특히 지도 학습(Supervised Learning)의 대표적인 문제 중 하나이다.
분류 문제의 다른 예시로는 다음과 같은 것들이 있다:
- 의료 진단: 환자의 증상, 검사 결과 등을 바탕으로 질병의 유무 또는 질병의 종류를 판단
- 손글씨 인식: 이미지로 주어진 손글씨를 0부터 9까지의 숫자 중 하나로 분류
- 감성 분석: 영화 리뷰, 상품 평가 등의 텍스트 데이터를 '긍정', '부정', '중립' 등의 감성 클래스로 분류
분류 문제는 클래스의 개수에 따라 이진 분류(Binary Classification)와 다중 클래스 분류(Multi-class Classification)로 나눌 수 있다. 이진 분류는 클래스가 2개인 경우(예: 스팸 여부 판단)이고, 다중 클래스 분류는 클래스가 3개 이상인 경우(예: 손글씨 인식)이다.
분류 모델의 성능은 정확도(Accuracy), 정밀도(Precision), 재현율(Recall), F1 스코어 등의 평가 지표를 사용하여 측정한다. 이러한 평가 지표를 통해 모델이 얼마나 정확하게 입력 데이터를 올바른 클래스로 분류하는지 판단할 수 있다.

소프트맥스
기존 이진 분류는 남자 또는 여자, 강아지인지 아닌지와 같이 0과 1로 매핑가능한 시그모이드 함수를 사용한다. 하지만 다중분류 문제와 같은 경우에는 시그모이드 함수로 분류하는데 한계가 존재한다.
소프트맥스(Softmax)는 딥러닝, 특히 다중 분류 문제에서 자주 사용되는 활성화 함수(Activation Function) 중 하나이다. 소프트맥스 함수는 입력받은 값들을 0과 1 사이의 확률 값으로 변환해주는 역할을 한다. 이렇게 변환된 값들의 총합은 항상 1이 되며, 이는 확률 분포를 나타낸다.
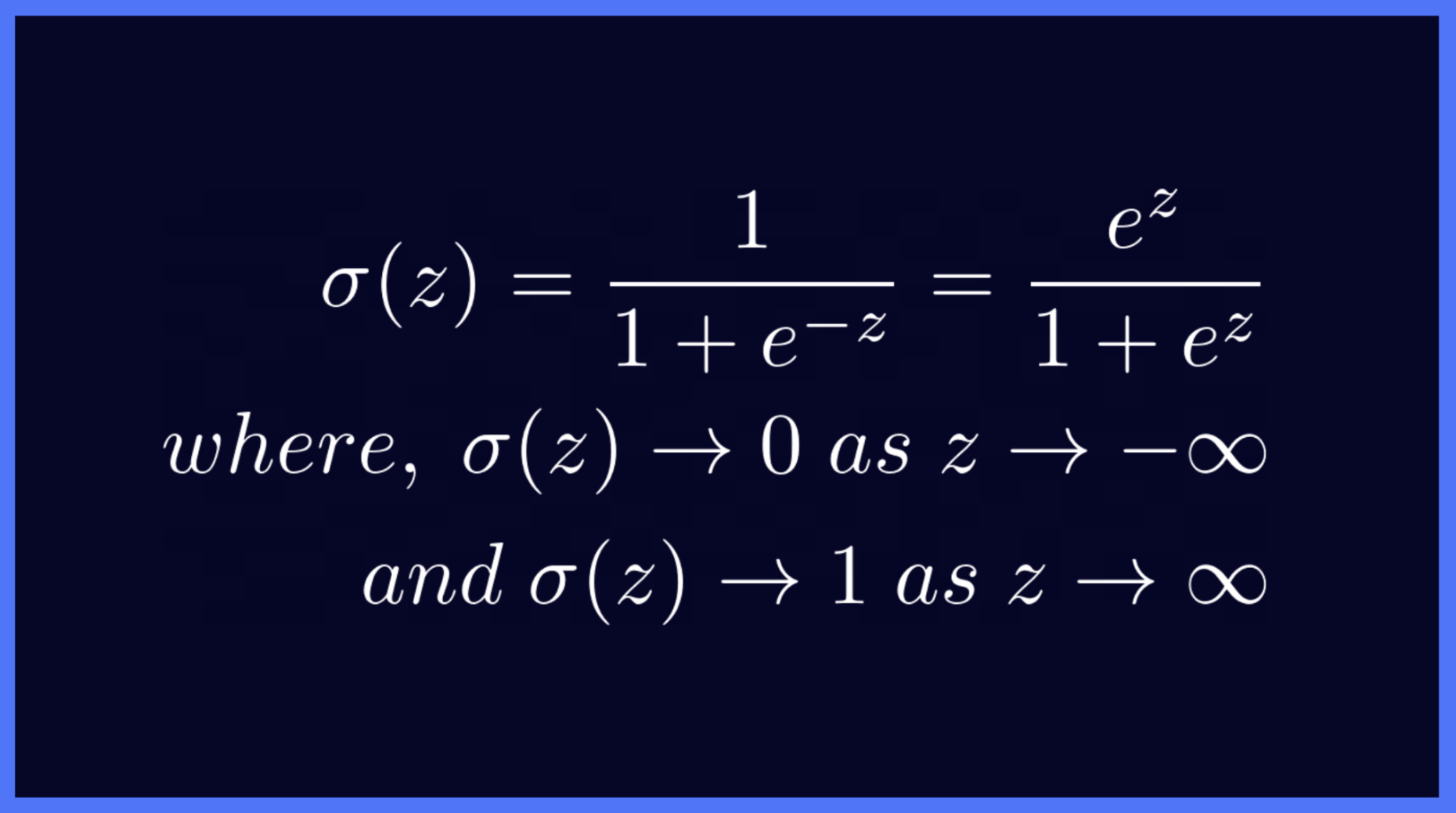
위 처럼 시그모이드 함수는 예측값이 높을 수록 1에 가깝고 낮을 수록 0에 가까운 값으로 매핑해준다.
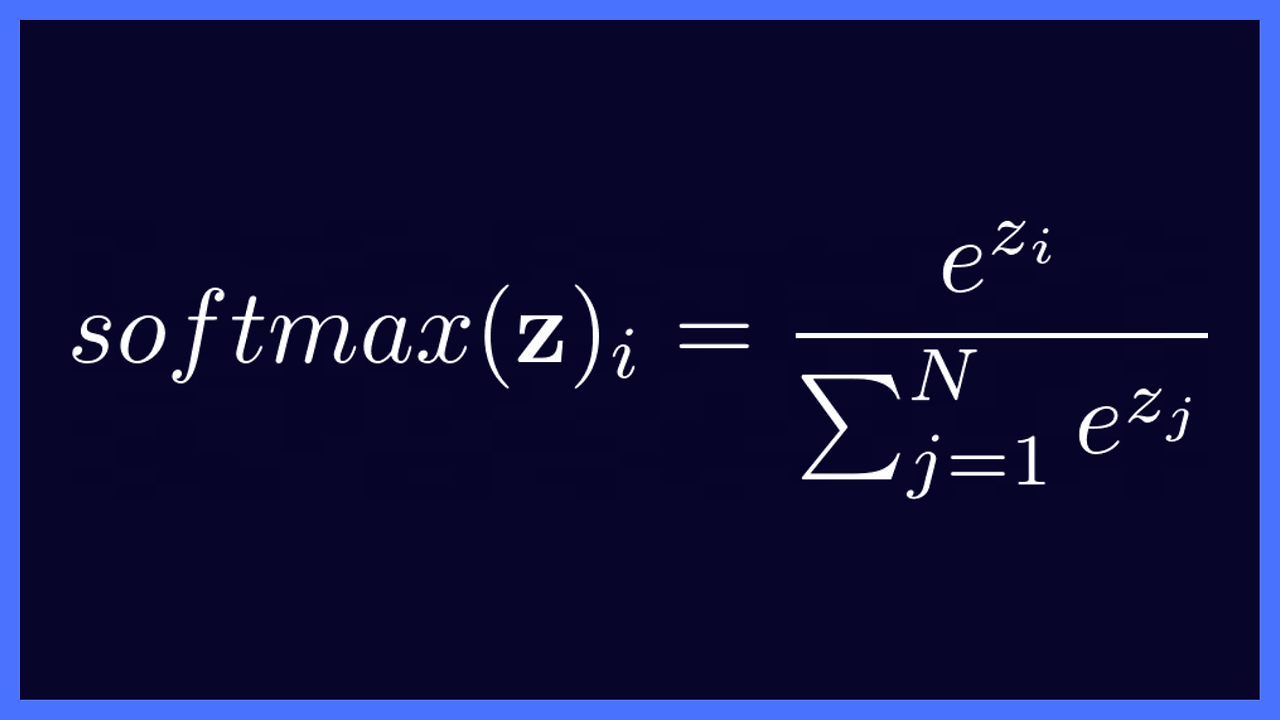
여기서 `z_i`는 입력 벡터 `z`의 i번째 원소를 나타내며, `exp()`는 지수 함수(exponential function)를 의미한다. 분모에 있는 `sum(exp(z_j))`는 입력 벡터 `z`의 모든 원소에 지수 함수를 적용한 값들의 합이다.
- 입력 벡터 `z`의 각 원소에 지수 함수를 적용한다. 이렇게 하면 모든 값이 양수가 되며, 값의 크기 차이가 더 커진다.
- 지수 함수를 적용한 값들의 총합을 계산한다.
- 각 원소를 총합으로 나눈다. 이렇게 하면 모든 값이 0과 1 사이의 값으로 변환되며, 총합은 1이 된다.
소프트맥스 함수의 장점
- 출력 값을 확률로 해석할 수 있다. 이는 분류 문제에서 각 클래스에 속할 확률을 나타내는 데 유용하다.
- 출력 값의 범위가 [0, 1]로 제한되므로, 출력 값의 스케일이 통일되어 안정적인 학습이 가능하다.
- 소프트맥스 함수는 미분 가능하므로, 역전파(backpropagation) 알고리즘에 사용할 수 있다.
소프트맥스 함수는 주로 신경망의 출력층에서 사용되며, 이진 분류 문제에서는 시그모이드 함수를 사용하기도 한다. 소프트맥스 함수를 통해 얻은 확률 값을 기반으로 가장 높은 확률을 가진 클래스를 선택하여 분류 문제를 해결할 수 있다.
예시
아래와 같이 3개의 클래스(물개, 판다, 오리)를 분류해야 하는 Task가 있다고 가정해보자 주어진 조건은 다음과 같다.
1. class = [물개, 판다, 오리]
2. z = [0.25, 1.23, -0.8]

이제 위 z값을 소프트맥스 함수에 넣어서 계산하면 다음과 같다.
1. 소프트맥스를 이용하여 물개 가능성 체크
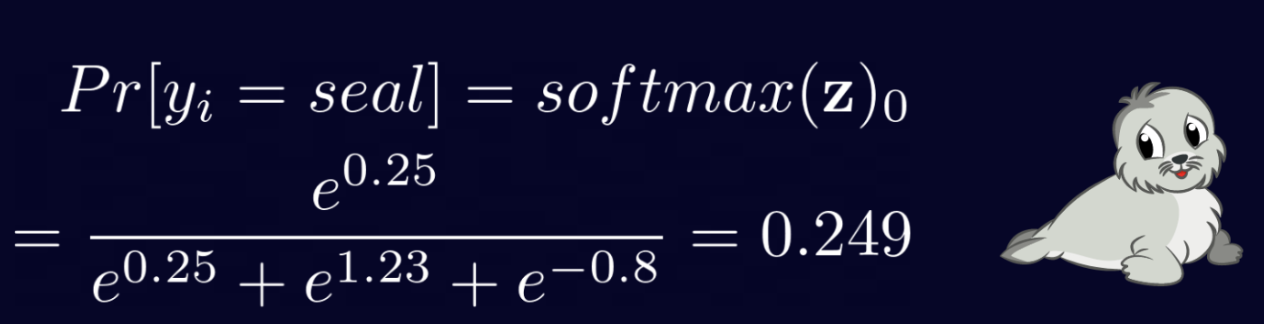
2. 소프트맥스를 이용하여 판다 가능성 체크

3. 소프트맥스를 이용하여 판다 가능성 체크
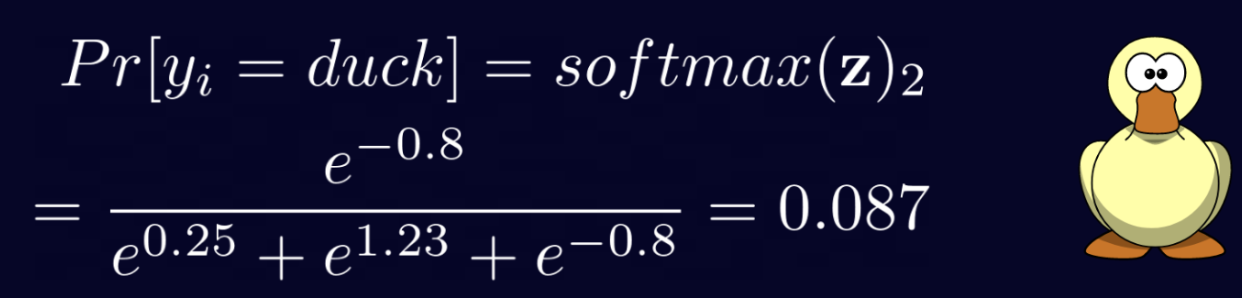
각각의 확률을 확인하면 [0.249, 0.664, 0.087]로 판다일 확률이 약 64퍼센트로 가장 높다

위 처럼 소프트맥스를 이용하면 z값들을 각각 확률값으로 바로 매핑할 수 있다!!
정리
이진 분류 Task에서 신경망을 통과한 예측값을 Sigmoid Function을 통과시켜 0과 1로 매핑을 시켰다.
- [0] , [1] -> 예시와 같이 각각의 스칼라값으로 매핑
하지만 다중 분류 Task에서는 0과 1로 매핑을 시키는데 한계가 존재하여 이를 SoftMax를 통해 원핫인코딩한 벡터로 매핑시킨다.
- [1, 0, 0], [0, 1, 0], [0, 0, 1] -> 예시와 같이 각각의 원핫 인코딩된 벡터로 매핑
위 처럼 벡터의 형태로 매핑하여 현재 신경망에서 나온 값을 다음과 같이 변환한다.
- 강아지 확률 -> 강아지 확률 / 모든 확률값
- 고양이 확률 -> 고양이 확률 / 모든 확률값
- 펭귄 확률 -> 펭귄 확률 / 모든 확률값
위와 같이 진행하면 가장 큰 확률을 가진 클래스를 분류할 수 있다.
'DeepLearning' 카테고리의 다른 글
| [손실함수] 다중 분류 Task에서 자주 사용되는 손실함수 크로스엔트로피(Cross-Entropy) (0) | 2024.04.16 |
|---|---|
| [Google Colab] 구글 드라이브 공유 파일 코랩에서 읽기(gdown) (0) | 2023.12.02 |
| NVIDIA 딥러닝 기초 9. 이미지개선 (0) | 2023.07.02 |



