주뇽's 저장소
백준(BOJ) 다이나믹 프로그래밍(DP) 계단 오르기 Silver 3 본문
https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

<그림 1>
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
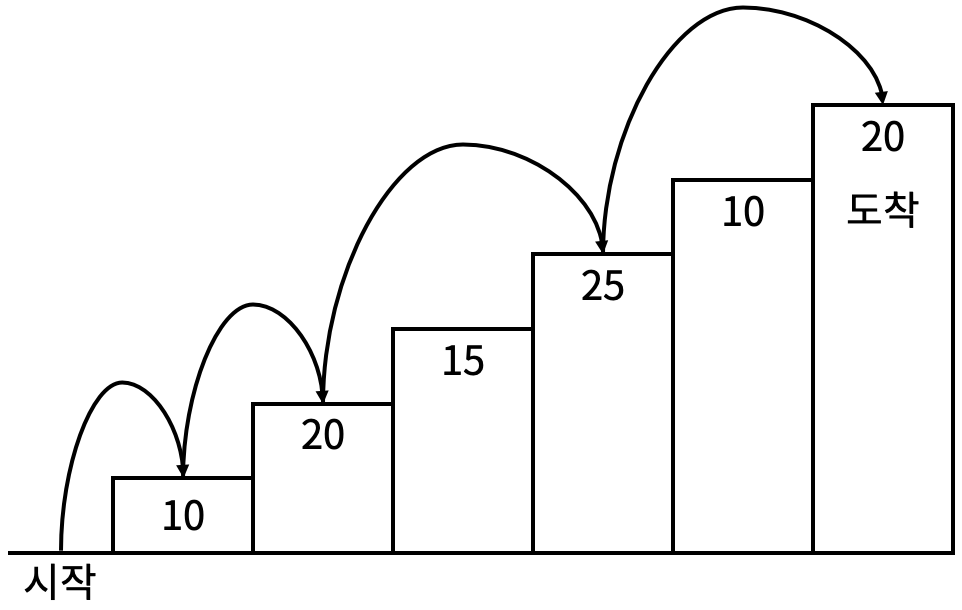
<그림 2>
계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
문제 해결
기본적인 DP문제이지만 1차원 배열이 아닌 2차원 배열을 사용하여 상태를 저장하는 방식으로 해결하는 문제이다.
이러한 접근법을 모르고 1차원 배열로 문제를 해결하려 했고 상당한 시간동안 고민만 하다가 해결하지 못했다. 다차원 배열을 이용하여 상태를 저장하는 이러한 방식은 알아두면 좋을것 같아 정리한다.
우선 해당 문제에서 상태는 총 3개이다.
1. 계단을 1개 밟음
2. 계단을 2개 연속으로 밟음
3. 계단을 밟지 않음
이제 위 3개의 상태를 관리할 다이나믹 테이블 이용해서 문제를 해결하면 된다.
문제와 같이 총 6개의 계단이 있다고 가정하자.
초기 테이블 상태
| 상태 \ 계단의 수 | 1개 | 2개 | 3개 | 4개 | 5개 | 6개 |
| 계단을 연속 밟음 | 10 | |||||
| 계단을 1개만 밟음 | 10 | |||||
| 계단을 밟지 않음 | 0 |
일단 초기 DP테이블은 위와 같다. 여기서 계단이 1개인 경우 계단을 연속으로 밟던 1개를 밟던 최댓값은 1개의 값이며, 계단을 밟지 않은 경우는 0이다.
계단이 2개인 테이블 상태
| 상태 \ 계단의 수 | 1개 | 2개 | 3개 | 4개 | 5개 | 6개 |
| 계단을 연속 밟음 | 10 | 10 + 20 | ||||
| 계단을 1개만 밟음 | 10 | 0 + 20 | ||||
| 계단을 밟지 않음 | 0 | max(10,10) |
테이블의 값을 갱신하는 식은 다음과 같다.
- 계단을 연속적으로 밟은 경우
계단을 연속적으로 밟으려면 이전 상태에서 계단을 1개 밟아야 한다. 따라서 아래와 같은 식이 만들어진다.
dp[연속계단] = dp[이전 1계단] + 현재 값- 계단을 1개만 밟는 경우
계단을 1개만 밝으려면 이전 상태에서 계단을 하나도 밟지 않아야 한다. 따라서 아래와 같은 식이 만들어진다.
dp[계단_1개] = dp[이전 0계단] + 현재 값- 계단을 0개만 밟는 경우
계단을 1개도 밟지 않은 경우는 이전 상태에서 연속적으로 밟거나 1개만 밟은 경우에서의 최댓값을 가져와야 한다.
dp[0계단] = max(dp[이전 1계단], dp[이전 연속계단])
위와 같은 방식으로 테이블을 갱신하면 다음과 같다
계단이 3개인 테이블 상태
| 상태 \ 계단의 수 | 1개 | 2개 | 3개 | 4개 | 5개 | 6개 |
| 계단을 연속 밟음 | 10 | 30 | 20 + 15 | |||
| 계단을 1개만 밟음 | 10 | 20 | 10 + 15 | |||
| 계단을 밟지 않음 | 0 | 10 | max(30,20) |
...
계단이 6개인 테이블 상태
| 상태 \ 계단의 수 | 1개 | 2개 | 3개 | 4개 | 5개 | 6개 |
| 계단을 연속 밟음 | 10 | 30 | 35 | 50 | 65 | 65 |
| 계단을 1개만 밟음 | 10 | 20 | 25 | 55 | 45 | 75 |
| 계단을 밟지 않음 | 0 | 30 | 30 | 35 | 55 | 65 |
모든 테이블을 갱신하면 위와 같은 테이블을 얻을 수 있다! 이 때 문제의 조건에서 마지막 계단은 반드시 밟아야 한다고 했으므로 계단을 가장 마지막 상태에서 계단을 밟지 않은 경우를 제외한 2가지 경우 중 최댓값인 75를 출력해주면 된다!
import sys
# sys.stdin = open("6.다이나믹프로그래밍/input.txt")
n = int(sys.stdin.readline())
dp = [[0 for _ in range(n+1)] for _ in range(3)]
stair = []
for _ in range(n):
stair.append(int(sys.stdin.readline()))
dp[0][1] = stair[0] #-- 연속
dp[1][1] = stair[0] #-- 밟
dp[2][1] = 0 #-- 안밟
if n<=1:
print(max(stair))
else:
for i in range(2, n+1):
#-- 연속 밟은경우 1칸 밟은 경우 + 자기 자신
dp[0][i] = dp[1][i-1] + stair[i-1]
#-- 처음 밟은 경우 0번 밟은 경우 + 자기 자신
dp[1][i] = dp[2][i-1] + stair[i-1]
#-- 안 밟은 경우 밟은 경우 중 최댓값
dp[2][i] = max(dp[0][i-1], dp[1][i-1])
print(max(dp[0][n], dp[1][n])) #-- 마지막은 밟아야 하므로 안 밟은 경우는 제외'알고리즘 > 동적계획법(DP)' 카테고리의 다른 글
| 스티커 (실버 1) [Class 4] (0) | 2024.04.05 |
|---|---|
| 백준(BOJ) 동적 프로그래밍 정수 삼각형 (1932) - Silver 1 (0) | 2023.09.13 |
| 백준(BOJ) 동적프로그래밍 RGB거리 (1149) - Silver 1 (0) | 2023.09.10 |



